Velocity – Time Graphs

A velocity-time graph shows how an object’s velocity (or speed) changes over time. The vertical axis (y-axis) represents speed, while the horizontal axis (x-axis) represents time.

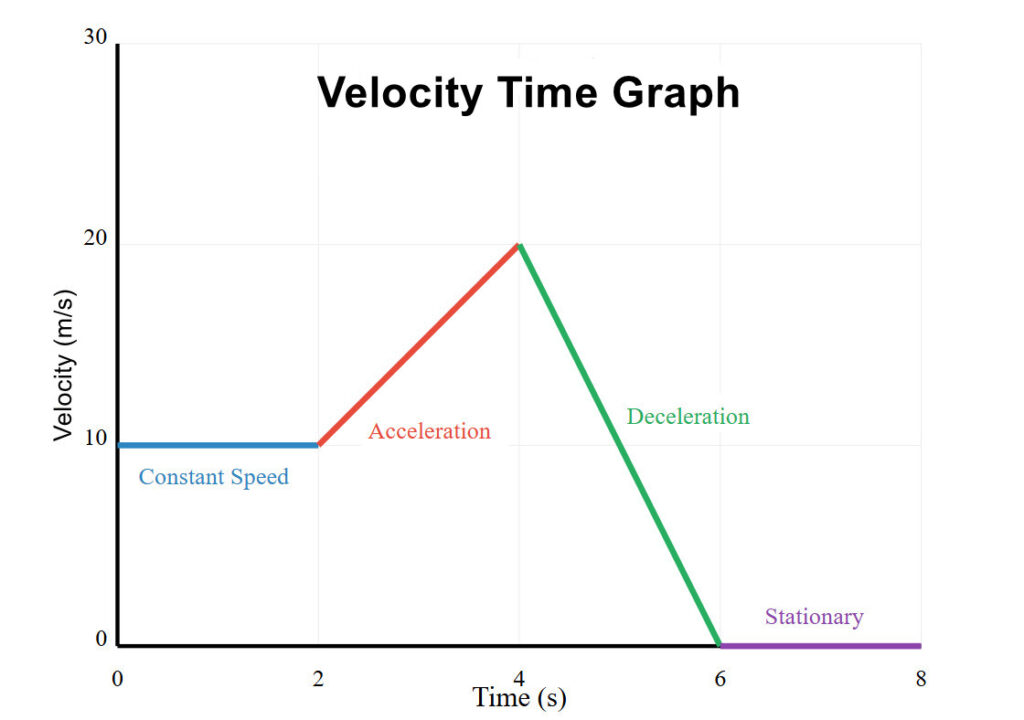
From the diagram above, we can see the following

1. Horizontal Line (Blue line)
   • Represents constant speed
   • No change in velocity
   • Area under this line represents distance traveled
2. Upward Slope (Red line)
   • Represents acceleration
   • Speed is increasing over time
   • The steeper the slope, the greater the acceleration
   • Area under this line represents distance traveled
3. Downward Slope (Green line)
   • Represents deceleration or negative acceleration
   • Speed is decreasing over time
   • The steeper the slope, the greater the deceleration
   • Area under this line represents distance traveled
4. Line at Zero (Purple line)
   • Represents an object at rest
   • No movement
   • Speed remains at zero
   • No distance is travelled

---

---

QUESTIONS #

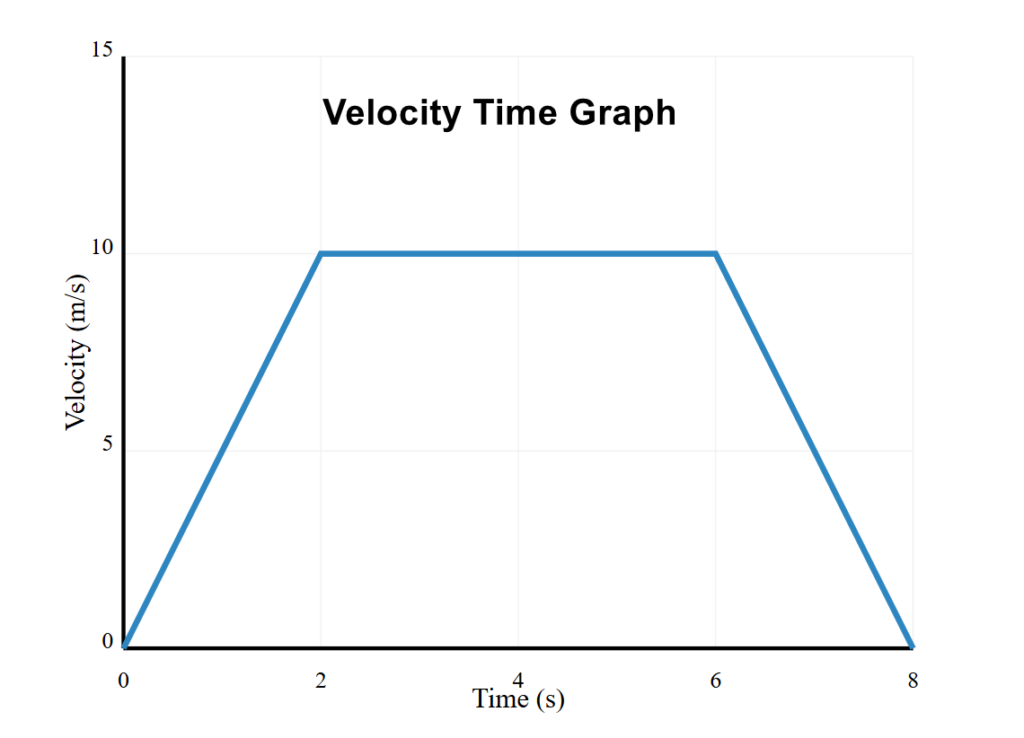
1. During which time period was the cyclist traveling at a constant speed?
2. What was the cyclist’s maximum speed during the journey?
3. Between 0 and 2 seconds, was the cyclist: a) Speeding up b) Slowing down c) Traveling at constant speed
4. Between 6 and 8 seconds, what was happening to the cyclist’s motion
5. For how many seconds did the cyclist maintain their top speed?
6. What is the total distance traveled during the entire 8-second journey? (Hint: find the total area under the curve)
7. During which 2-second interval did the cyclist cover the greatest distance? a) 0-2 seconds b) 2-4 seconds c) 4-6 seconds d) 6-8 seconds
8. How far did the cyclist travel between 2-6 seconds? (Hint: this is the area of a rectangle)

---

ANSWERS #

1. The cyclist traveled at constant speed between 2-6 seconds (this is shown by the horizontal line segment)
2. The maximum speed was 10 m/s (shown on the y-axis where the horizontal line segment is)
3. Answer: a) Speeding up (The line goes up from 0 to 10 m/s, showing acceleration/speeding up)
4. Between 6-8 seconds, the cyclist was slowing down (decelerating), shown by the downward slope back to 0 m/s
5. The cyclist maintained their top speed of 10 m/s for 4 seconds (from time=2s to time=6s)
6. Total distance calculation:
   • First section (0-2s): Triangle = ½ × 2s × 10m/s = 10m
   • Middle section (2-6s): Rectangle = 4s × 10m/s = 40m
   • Last section (6-8s): Triangle = ½ × 2s × 10m/s = 10m Total distance = 10 + 40 + 10 = 60 meters
7. Answer: b) 2-4 seconds Explanation: During this time the cyclist maintained their highest speed (10 m/s) for the full 2 seconds, covering 20 meters. All other 2-second intervals either involved acceleration, deceleration, or lower speeds.
8. Distance between 2-6 seconds = 40 meters Calculation: Area of rectangle = speed × time = 10 m/s × 4s = 40m

These